Support:Documents:Examples:Estimate Input Delay and Rate Constants

Estimating Input Delay and Rate Constants

This example demonstrates an approach to simultaneously estimating input function delay along with parameters of the 1-tissue compartment (e.g. blood flow) model. For the sake of generality, the This could be interpreted as a

Tissue uptake

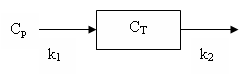
This model has one tissue compartment. Material in the blood is assumed to rapidly exchange with that in (extravascular) tissue. The tissue model has two rate constants: K₁ and k₂ and is depicted in the diagram:

It can also be described by the differential equation:

dC_T/dt = K₁ C_p - k₂ C_T

where C_T is the tissue concentration and C_p is the plasma concentration of radioactive water. C_T and C_p are interpreted as either molar concentrations (Salinas, Muzic and Saidel 2007).

Input function

This example also demonstrates how to temporally align measured input function data to the tissue (image) data. Here the plasma concentration vs. time t is modeled as

C_p(t, tau) = M(t-d) if t >= tau; 0 if t < tau .

M(t) is the measured input data, tau is the delay parameter to estimate, and t is the time in minutes.

Because the delay tau is estimated in this example, it will be handy to note that derivative of the input with respect to delay is

C_p(t)/d tau = - dM/dt|_t-tau

For this example, M is determined by using linear interpolation to interpolate between measured values. The interpolation is implemented using piecewise polynomial framework (and it could be easily modified to accommodate cubic spline interpolation).

Let inputData be a two-column matrix with column 1 holding sample times and column 2 holding the sampled input concentrations.

The interpolation coefficients may be calculated using the lspline function

ppM = lspline(inputData(:,1), inputData(:,2));

To evaluate the derivative dC_p/dt, which can be determined in terms of dM/dt by analytically differentiating the interpolating polynomial.

[breaks, coefs, l, k, d] = unmkpp(ppM);
ppdMdtau = mkpp(breaks, repmat(k-1:-1:1,d*l,1) .* coefs(:,1:k-1), d);

Bucks, explain how this works

The input function is then implemented as

function [Cp, dCpdtau] = DelayExampleInput(parm, t, X)
if (nargout > 0),
    t = t(:); % ensure t is a column vector
    tau = parm(1);  % delay
    ppC = X{1}; % piecewise-polynomial coefficients for Cp
    Cp = zeros(size(t));
    f = find(t > tau);
    Cp(f) = ppval(ppC, t(f) - tau);

    if (nargout > 1),
        ppdCdt = X{2}; % piecewise-polynomial coefficients for derivative
        dCpdtau = zeros(size(t));
        dCpdtau(f) = -ppval(ppdCdt, t(f) - tau);
    end
end

Pixel values

In this example, the pixel values are assumed to represent measurements of C_T. (To keep the example simple, intravascular concentration of tracer is ignored.) The values of the parameters p = [K₁; k₂; tau] will be estimated.

Implement the Compartment Model

Create a new model

more sections...

Fit Data

Plot the results and make the figure below for this wiki