Support:Documents:Examples:FDG with Time-varying Rate Constants

FDG Model with Time-varying Rate Constants

This example demonstrates how to implement the two-tissue compartment model with extended such that K1 and k2 vary in time.

This models the case where there are physiologic changes during the course of the PET scanning. This might happen if tumors are being treated during scanning.

Tissue uptake

This model was described by Huang and Phelps.

MAKE FIGURE

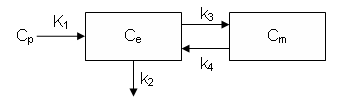
It can also be described by the differential equations:

dC_e/dt = K₁ C_p - k₂ C_e - k₃ C_e + k₄ C_m

dC_m/dt = k₃ C_e - k₄ C_m

C_e is the tissue concentration of FDG and C_m as the tissue concentration of metabolized FDG (FDG-6-phosphate)

C_e and C_m are interpreted as molar concentrations (Salinas, Muzic and Saidel 2007).

In the standard model. the rate constants K₁, k₂, k₃ and k₄ are assumed to be independent of time.

Here we allow K₁ and k₂ to be a linear function of time:

K₁(t) = K₁⁰ + a t

k₂(t) = K₂⁰ + b t

To implement the time-varying rate constants, it is necessary to

Implement the Compartment Model

Create a new model

First create an new model stored in variable bfcm (blood flow compartment model) and add compartments. The J compartment is not shown in the figure above but is needed to accept the flux from the k₂ arrow.

% create new, empty model
bfcm = compartmentModel; 
 
% add compartments
bfcm = addCompartment(bfcm, 'CT');
bfcm = addCompartment(bfcm, 'J');

Specify the input

The specific activity (ratio of activity to molar concentration) is an exponentially decaying function S(t) = S₀ exp(-0.341 t) where t is expressed in units of minutes and 0.341 = ln(2)/half-life of ¹⁵O and S₀ is the specific activity at time t = 0.

% define the initial specific activity and decay constant
sa0 = 1; % specific activity at t=0
dk = 0.341; % O-15 decay constant

Next specify the input functions C_p and C_a for the compartment model. fin is the name of the function that implements Feng input. pCp and pCa are parameter vectors that hold the values of p₁, p₂, ... p₆ for C_p and C_a.

bfcm = addInput(bfcm, 'Cp', sa0, dk, 'fin', 'pCp');
bfcm = addParameter(bfcm, 'pCp', 2*[851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5]);

bfcm = addInput(bfcm, 'Ca', sa0, dk, 'fin', 'pCa');
bfcm = addParameter(bfcm, 'pCa', [851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5]);

Define the connections (arrows) between the compartment and input. The link type 'L' indicates linear kinetics from an input to a compartment and type 'K' indicates linear kinetics from one compartment to another.

% connect compartments and inputs
bfcm = addLink(bfcm, 'L', 'Cp', 'CT', 'K1');
bfcm = addLink(bfcm, 'K', 'CT', 'J', 'k2');
 
% define values for K1, k2 ...
bfcm = addParameter(bfcm, 'K1', 'F');
bfcm = addParameter(bfcm, 'k2', 'K1/lambda');
bfcm = addParameter(bfcm, 'F', 0.5);
bfcm = addParameter(bfcm, 'lambda', 1.0);
bfcm = addParameter(bfcm, 'Fv', 0.05);

Define tissue and blood outputs

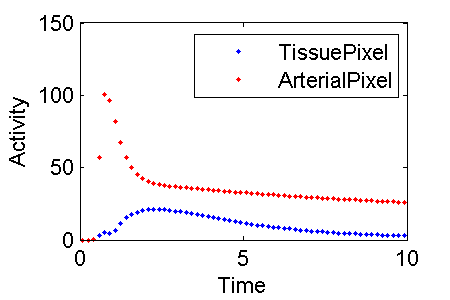
Define two model outputs. The output called TissuePixel predicts the activity in a tissue pixel and the output called ArterialPixel predicts the activity that would be observed in a pixel in the aorta. TissuePixel corresponds to C_TS + F_vC_a whereas ArterialPixel is 100% C_a.

% define the activity concentration in tissue pixel
bfcm = addOutput(bfcm, 'TissuePixel', {'CT', '1'}, {'Ca', 'Fv'});
 
% define the activity concentration in arterial blood pixel
bfcm = addOutput(bfcm, 'ArterialPixel', {'CT', '0'}, {'Ca', '1'});

Note that COMKAT even accounts for the time-averaging of concentrations over the durations of the scan frames. For simplicity here a sequence of contiguous 10-second frames is used. (Frame start times 0, 10, 20, ... 590 sec and frame end times 10, 20, 30, ... 600 sec).

% specify scan frame times
bfcm = set(bfcm, 'ScanTime', [[0:10:590]' [10:10:600]']/60); % division by 60 converts sec to min

Solve for the model output

Finally, tell COMKAT to solve the model to obtain simulation data that will be used in fitting.

[PET, PETIndex, Output, OutputIndex] = solve(bfcm);

% plot activity in tissue PET(:,3) and blood PET(:,4)
midTime = (PET(:,1) + PET(:,2)) / 2;
plot(midTime, PET(:,3), 'b-', midTime, PET(:,4), 'r.')
legend(PETIndex{3}, PETIndex{4})

% make the figure for this wiki
set(1,'PaperPosition',[0.25 2.5 3 2])
print -dpng c:\temp\ExampleFigureBloodFlowInputModelDataToFit.png

Note, different rows of PET correspond to different frames. The columns of PET hold various quantities as indicated in PETIndex. That is, the contents of column i are described in PETIndex{i}.

Fit Data

Modify the COMKAT model a bit so that it can be used to fit data created above.

Specify the data to fit

Just use the result from above.

data = PET(:, [3 4]);
bfcm = set(bfcm, 'ExperimentalData', data);

Specify parameters to estimate along with their initial guesses and range of feasible values.

% specify parameters to estimate
bfcm = addSensitivity(bfcm, 'pCp', 'F');

% define initial guess and lower and upper bounds
pCpInit = 0.9*2*[851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5];
FInit = 0.3;
pinit = [pCpInit FInit];
lb = [2*[85 2 2 -8 -3 -0.1 .05] 0.1];
ub = [2*[2000 100 200 -1 -0.01 -0.001 2] 1.];

Note the values of the initial guesses for the input function parameters are 0.9 times the true values. (We're are not cheating by starting with the correct values.)

Do the actual fitting

Fit the data to estimate values of the parameters

[pEst, modelFit] = fit(bfcm, pInit, lb,ub);

COMKAT makes fitting easy!

Plot the results and make the figure below for this wiki

plot(midTime, modelFit(:,1), 'b', midTime, PET(:,3), 'b.', midTime, modelFit(:,2), 'r', midTime, PET(:,4), 'r.')
legend('Tissue Fit', PETIndex{3}, 'Arterial Fit', PETIndex{4})
xlabel('Time')
ylabel('Activity')
print -dpng c:\temp\ExampleFigureBloodFlowInputModelFit.png

Ta Da

It looks like a pretty good fit.