Support:Documents:Examples:Estimate Change of Neurotransmitter

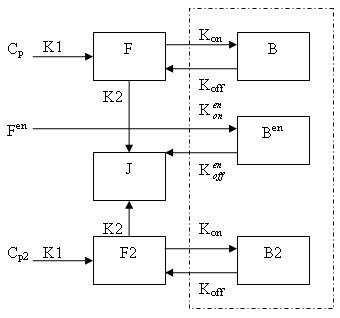
Model of Neurotransmitter PET (ntPET)

Overview

The changes of endogenous neurotransmitter by PET scanning after a stimulus have been proved with different approaches. In stead of detecting the increase or decrease of a neurotransmitter, it is important to characterize the temporal change of a neurotransmitter after a stimulus. Morris proposed the new technique (called ntPET) for capturing the dynamic changes of a neurotransmitter after a stimulus and demonstrated the ability of this method to reconstruct the temporal characteristics of an enhance in neurotransmitter concentration.

Generally, there are two separate injections of tracer for ntPET: one for the rest condition (without any stimuli) and the other for the activation condition (after a stimulus). Therefore, the model can be described as:

This model can be described by the differential equations:

dF/dt = K₁C_p - K₂F - K_on[B_max - B - B2 - B^en]F + k_offB

dB/dt = K_on[B_max - B - B2 - B^en]F - k_offB

dF2/dt = K₁C_p2 - K₂F2 - K_on[B_max - B - B2 - B^en]F2 + k_offB2

dB2/dt = K_on[B_max - B - B2 - B^en]F2 - k_offB2

dB^en/dt = K^en_on[B_max - B - B2 - B^en]F^en -k^en_offB^en

C_p is the plasma concentration of tracer at the first injection (the "rest" condition).

F and B are free (unbound) and bound molar concentrations of tracer after the first injection

C_p2 is the plasma concentration of tracer at the second injection (the "activation" condition).

F2 and B2 are free (unbound) and bound molar concentrations of tracer after the second injection.

F^en and B^en are free and bound molar concentrations of a neurotransmitter released by endogenous ligand after a stimulus.

B_max is the maximum number of receptors that can be bound by neurotransmitter or tracer.

B_max - B - B2 - B^en is the concentration of available receptors. This also indicates that binding is saturable.

K₁, K₂, K_on, K_off, K^en_on and K^en_off are rate constants.

Implementing the Compartment Model

Create a new model for ntPET

   %MODEL CONSTRUCTION   
    cm = compartmentModel;

   % Set scan time
    inj2Delay = 240; % min between 1st and 2nd inj
    disp('Define one long study: inj 1 = baseline, inj 2 = activation');
    scantInj1 = [[0:0.1:0.9 1:0.25:1.75 2:0.5:4.5 5:1:59]' [0.1:0.1:1 1.25:0.25:2 2.5:0.5:5 6:1:60]']; 
    scantInj2 = scantInj1 + inj2Delay;
    scant = [scantInj1; scantInj2]; 
    deltaT = scant(:,2) - scant(:,1);
    tmid   = 0.5*(scant(:,1) + scant(:,2));

    %Set parameters of the model
    cm = addParameter(cm, 'PV', 1 );    
    cm = addParameter(cm, 'Fv', 0);     
    cm = addParameter(cm, 'sa', 1);    % uCi/pmol
    cm = addParameter(cm, 'dk', 0);    % assume data are decay-corrected        
    cm = addParameter(cm, 'k1',      0.9);   
    cm = addParameter(cm, 'k2',      0.4);   
    cm = addParameter(cm, 'kon' ,   0.01);   
    cm = addParameter(cm, 'koff',    0.14);  
    cm = addParameter(cm, 'k2ref',  0.3);
    cm = addParameter(cm, 'Bmax',  80);
    cm = addParameter(cm, 'konEN', 0.25);
    cm = addParameter(cm, 'koffEN', 25);     

    %model for baseline condition:
    cm = addCompartment(cm, 'F');
    cm = addCompartment(cm, 'B',      'Bmax');
    cm = addCompartment(cm, 'Junk');

    %model for activation condition:
    cm = addCompartment(cm, 'F2');
    cm = addCompartment(cm, 'B2',      'Bmax');
    cm = addCompartment(cm, 'B^{EN}', 'Bmax');

    % Create input functions for two injections
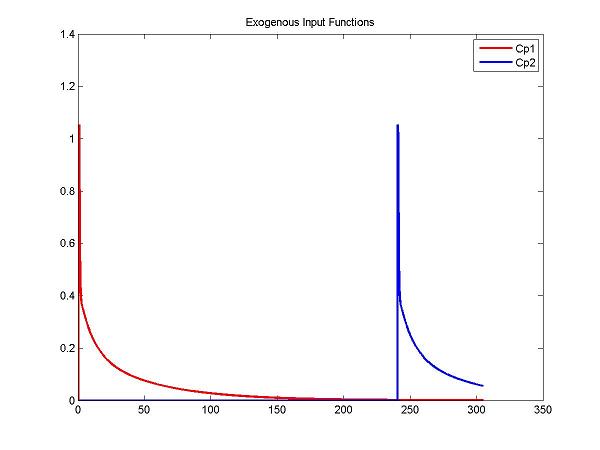
    t = 0:0.05:305; % coverage out to 6+ h
    Cp1Data = fengInput([2 0.5 8.5 0.22 0.2 -4. -0.1 -0.02], t);
    Cp2Data = fengInput([2 inj2Delay+0.5 8.5 0.22 0.2 -4. -0.1 -0.02], t);
    ppCp1 = spline(t, Cp1Data);
    ppCp2 = spline(t, Cp2Data);
    
    figure; plot(t, ppval(ppCp1, t), 'r', t, ppval(ppCp2,t), 'b', 'LineWidth', 2); title('Exogenous Input Functions'); legend('Cp1', 'Cp2')

    cm = addInput(cm, 'C_p', 'sa', 'dk', 'ppval', ppCp1);
    cm = addInput(cm, 'C_p2', 'sa', 'dk', 'ppval', ppCp2);

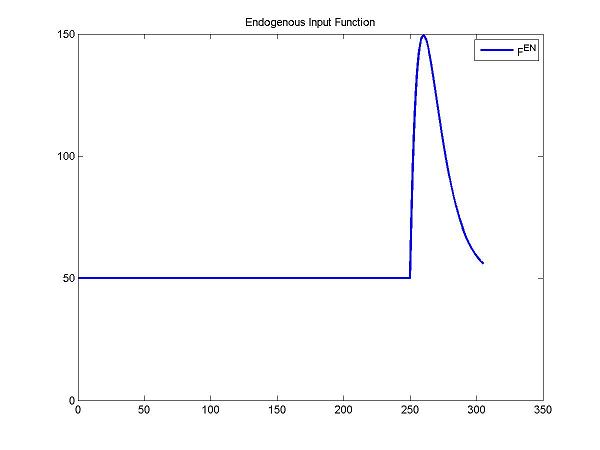
Here, we simulate the endogenous input function (after a stimulus) by a gamma variate function. F^en = Basal + Gamma[t-Delay]^Alpha exp(-Beta[t-Delay]). Note: Basal is the concentration of the endogenous neurotransmitter without any stimulus. Gamma, Alpha and Beta control the change of concentrations of the endogenous neurotransmitter. Delay is the delay time.

    DApar = [50 27 1 0.1 240+10]; % = [Basal Gamma Alpha Beta Delay] 
    cm = addParameter(cm, 'DA', DApar);
    cm = addInput(cm, 'F^{EN}', 0, 0, 'gamma', 'DA'); %DA defined by gamma variate function at activation condition
    figure; plot(t, gamma(DApar, t), 'b', 'LineWidth', 2); title('Endogenous Input Function'); legend('F^{en}'); 
    ax = axis; axis([ax(1) ax(2) 0 ax(4)]); % ensure minimum y-axis value is zero