Difference between revisions of "Support:Documents:Examples:Estimate Change of Neurotransmitter"
| Line 12: | Line 12: | ||
This model can be described by the differential equations: | This model can be described by the differential equations: | ||
| − | dF/dt=K<sub>1<sub>C<sub>p<sub>-K<sub>2<sub>F-K<sub>on<sub>[b<sub>max<sub>-B-B<sup>en<sup>] | + | dF/dt = K<sub>1<sub> C<sub>p<sub> - K<sub>2<sub> F - K<sub>on<sub> [b<sub>max<sub> - B -B2 - B<sup>en<sup>] |
Revision as of 19:10, 25 February 2009
Model of Neurotransmitter PET (ntPET)
Overview
The changes of endogenous neurotransmitter by PET scanning after a stimulus has been proved with different approaches. In stead of detecting the increase or decrease of a neurotransmitter, it is important to characterize the temporal change of a neurotransmitter after a stimulus. Morris proposed the new technique (called ntPET) for capturing the dynamic changes of a neurotransmitter after a stimulus and demonstrated the ability of this method to reconstruct the temporal characteistics of an enhance in neurotransmitter concentration.
Here we present a general model of ntPET, which can be simplified to Morris' model.
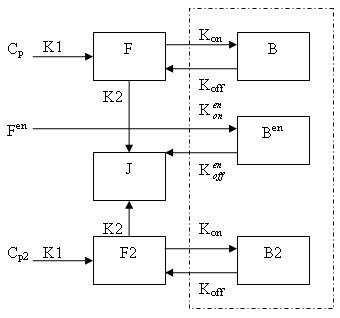
Generally, there are two separate injections of tracer for ntPET: one for the rest condition (without any stimuli) and the other for the activation conditon (after a stimulus). Cp is the pasma concentration of tracer at the first injection (the "rest" condition), F and B are free (unbound) and bound molar concentrations of tracer after the first injection Cp2 is the pasma concentration of tracer at the second injection (the "activation" condition), F2 and B2 are free (unbound) and bound molar concentrations of tracer after the second injection. Fen and Ben are free and bound molar concentrations of a neurotransmitter released by endogenous ligand after a stimulus.
This model can be described by the differential equations:
dF/dt = K1 Cp - K2 F - Kon [bmax - B -B2 - Ben]