Difference between revisions of "Support:Documents:Examples:Estimate physiological parameters using a physiologically based model"
Jump to navigation
Jump to search
| Line 3: | Line 3: | ||
===Overview=== | ===Overview=== | ||
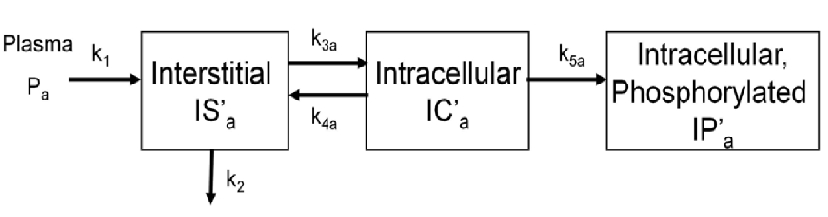
| − | To evalute glucose trasnport and phosphorylation in skeletal muscle,[http://online.medphys.org/resource/1/mphya6/v38/i8/p4587_s1 a physiologically based model] has been proposed by our group. | + | To evalute glucose trasnport and phosphorylation in skeletal muscle,[http://online.medphys.org/resource/1/mphya6/v38/i8/p4587_s1 a physiologically based model] has been proposed by our group. The below figure shows the kinetics of a phosphorylatable glucsoe analog (e.g.g ^1^8^F-labeled 2-fluoro-2-deoxy-D-glucose) in skeletal muscle. |
[[Image:Example-fig.jpg]] | [[Image:Example-fig.jpg]] | ||
Revision as of 18:56, 22 August 2011
Estimation of Physiological Parameters Using a Physiologically Based Model
Overview
To evalute glucose trasnport and phosphorylation in skeletal muscle,a physiologically based model has been proposed by our group. The below figure shows the kinetics of a phosphorylatable glucsoe analog (e.g.g ^1^8^F-labeled 2-fluoro-2-deoxy-D-glucose) in skeletal muscle.
Here, we show an example of implementation of the proposed model using COMKAT.
Example of Implementation of the Physiologically Based Model
cm=compartmentModel;
% Define parameters
cm=addParameter(cm,'k1',0.1);
cm=addParameter(cm,'k2','k1/Fis');
cm=addParameter(cm,'k3','VG/(Fis*KGa+Fis*ISg*KGa/KGg)');
cm=addParameter(cm,'k4','VG/(Fic*KGa+Fic*ICg*KGa/KGg)');
cm=addParameter(cm,'k5','VH/(Fic*KHa+Fic*ICg*KHa/KHg)');
cm=addParameter(cm,'Fb',0.02); % fraction of total space occupied by blood
cm=addParameter(cm,'Fis',0.3); % fraction of total space occupied by interstitial space
cm=addParameter(cm,'Fic','1-Fis-Fb'); % fraction of total space occupied by intracellular space
cm=addParameter(cm,'F',1);
cm=addParameter(cm,'Pg',6); % Plasma glucose concentration (mM)
cm=addParameter(cm,'ISg',5.4); % Interstitial glucose concentration (mM)
cm=addParameter(cm,'ICg',0.2); % Intracellular glucose concentration (mM)
cm=addParameter(cm,'KGg',3.5); % Michaelis constant of glucose transporter (GLUT) for glucose (mM)
cm=addParameter(cm,'KHg',0.13); % Michaelis constant of hexokinase for glucose (mM)
cm=addParameter(cm,'KGa',14); % Michaelis constant of glucose transporter (GLUT) for glucose analog (mM)
cm=addParameter(cm,'KHa',0.17); % Michaelis constant of hexokinase for glucose analog (mM)
cm=addParameter(cm,'VG','(k1*Pg-k1*ISg)/(ISg/(KGg+ISg)-ICg/(KGg+ICg))'); % Maximal velocity of glucose transport for glucose=6FDG=2FDG
cm=addParameter(cm,'VH','(k1*Pg-k1*ISg)/(ICg/(KHg+ICg))'); % Maximal velocity of glucose phosphorylation for glucose=6FDG=2FDG
% Specific activity (sa): if the unit of image data is the same with that of input function, the specific activity is 1.
cm=addParameter(cm,'sa',1);
% Usually, the decay time correction of image data is performed. So, dk is zero.
cm=addParameter(cm,'dk',0);
% Define scan time
delay = 0.0;
scanduration = 120;
t=[ones(5,1)/30;ones(10,1)/12;ones(12,1)*0.5;ones(8,1);ones(21,1)*5];
scant = [[0;cumsum(t(1:(length(t)-1)))] cumsum(t)];
scanTime = [scant(:,1),scant(:,2)];
cm = set(cm, 'ScanTime', scanTime);
lambda = [-12.02 -2.57 -0.02];
a = [1771.5 94.55 14.27];
cm = addParameter(cm, 'pfeng', [delay a lambda]');
cm = addInput(cm, 'Cp', 'sa', 'dk', 'fengInputByPar','pfeng'); % Cp is the plasma input function
cm = addInput(cm, 'Ca',1,0, 'fengInputByPar', 'pfeng'); % Ca is the decay-corrected whole-blood input function. Herein, we assume that Cp=Ca.
% Define compartment
cm=addCompartment(cm,'IS'); % interstitial
cm=addCompartment(cm,'IC'); % intracellular
cm=addCompartment(cm,'IP'); % intracellular phosphorylated
cm=addCompartment(cm,'Junk');
% Define link
cm=addLink(cm,'L','Cp','IS','k1');
cm=addLink(cm,'K','IS','Junk','k2');
cm=addLink(cm,'K','IS','IC','k3');
cm=addLink(cm,'K','IC','IS','k4');
cm=addLink(cm,'K','IC','IP','k5');
% Define output obtained from each normalized compartment
wlistTotal={'IS','F';'IC','F';'IP','F'};
xlistTotal={'Ca','Fb'};
cm=addOutput(cm,'TissueTotal',wlistTotal,xlistTotal);
cm=addSensitivity(cm,'k1','ISg','ICg','Fis','Fb');
[PET,PETIndex,Output,OutputIndex]=solve(cm);
noise_level=0.05;
sd=noise_level*sqrt(PET(:,3)./(PET(:,2)-PET(:,1)));
data=sd.*randn(size(PET(:,3)))+PET(:,3);
cm=set(cm,'ExperimentalData',data);
cm = set(cm,'ExperimentalDataSD',sd);
optsIRLS = setopt('SDModelFunction', @IRLSnoiseModel);
cm = set(cm, 'IRLSOptions', optsIRLS);
oo = optimset('TolFun', 1e-8, 'TolX', 1e-4,'Algorithm','interior-point');
cm = set(cm, 'OptimizerOptions', oo);
% Set initial conditions and boundary conditions
% k1, ISg, ICg, Fs, Fv
pinit = [0.01 ; 4.4 ; 0.1 ;0.15 ; 0.01];
plb = [0.001; 1 ; 0.001;0.10 ; 0 ];
pub = [0.5 ; 6 ; 1 ;0.60 ; 0.04];
[pfit, qfit, modelfit, exitflag, output, lambda, grad, hessian, objfunval] = fitGen(cm, pinit, plb, pub, 'IRLS');
figure;
t = 0.5*(PET(:,1)+PET(:,2));
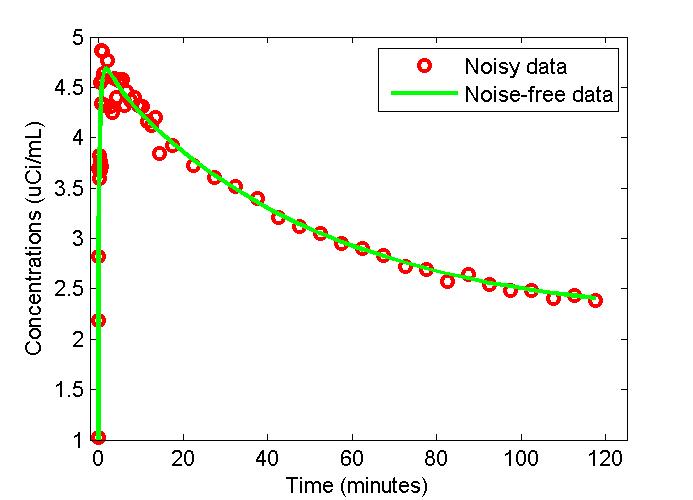
plot(t,PET(:,3),'g-',t,data,'ro','LineWidth',2);
xlabel('Time (minutes)');
ylabel('Concentrations (uCi/mL)');
legend('Noisy data','Noise-free data');
figure;
t = 0.5*(PET(:,1)+PET(:,2));
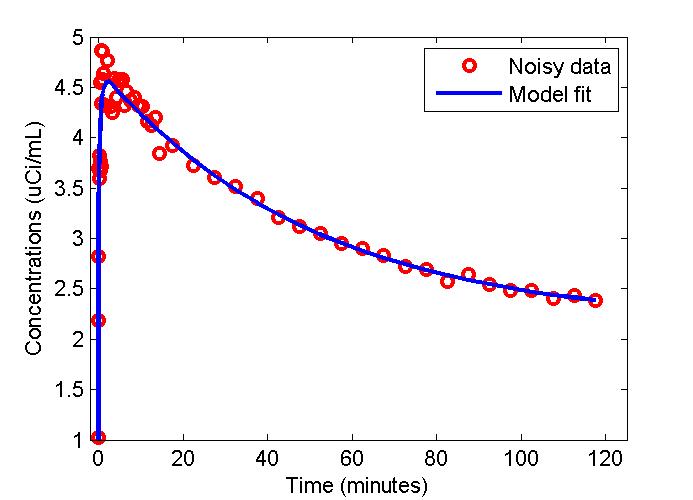
plot(t,data,'ro',t,modelfit,'b-','LineWidth',2);
xlabel('Time (minutes)');
ylabel('Concentrations (uCi/mL)');
legend('Noisy data', 'Model fit');
Pg=6;KGa=14;KHa=0.17;KGg=3.5;KHg=0.13; % Unit is mM
k1=pfit(1);k2=pfit(1)/pfit(4);ISg=pfit(2);ICg=pfit(3);Fis=pfit(4);Fb=pfit(5);
VG=(k1*ISg-k1*Pg)/(ICg/(KGg+ICg)-ISg/(KGg+ISg))
VH=(k1*Pg-k1*ISg)/(ICg/(KHg+ICg))
CI=VG*ISg/(KGg+ISg)
CE=VG*ICg/(KGg+ICg)
PR=VH*ICg/(KHg+ICg)