Support:Documents:Examples:Estimate Change of Neurotransmitter

Overview

The changes of endogenous neurotransmitter by PET scanning after a stimulus has been proved with different approaches. In stead of detecting the increase or decrease of a neurotransmitter, it is important to characterize the temporal change of a neurotransmitter after a stimulus. Morris proposed the new technique (called ntPET) for capturing the dynamic changes of a neurotransmitter after a stimulus and demonstrated the ability of this method to reconstruct the temporal characteistics of an enhance in neurotransmitter concentration.

Here we present a general model of ntPET, which can be simplified to Morris' model.

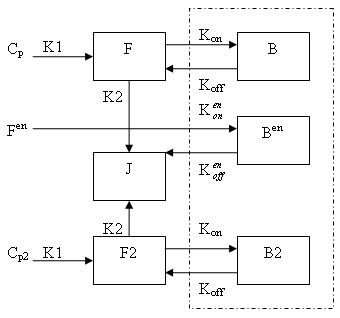
This model can be described by the differential equations:

dF/dt = K₁C_p - K₂F - K_on[B_max - B -B2 - B^en]F + k_offB

dB/dt = K_on[B_max - B -B2 - B^en]F - k_offB

Generally, there are two separate injections of tracer for ntPET: one for the rest condition (without any stimuli) and the other for the activation conditon (after a stimulus).

C_p is the pasma concentration of tracer at the first injection (the "rest" condition).

F and B are free (unbound) and bound molar concentrations of tracer after the first injection

C_p2 is the pasma concentration of tracer at the second injection (the "activation" condition).

F2 and B2 are free (unbound) and bound molar concentrations of tracer after the second injection.

F^en and B^en are free and bound molar concentrations of a neurotransmitter released by endogenous ligand after a stimulus.