Difference between revisions of "Support:Documents:Examples:FDG with Time-varying Rate Constants"
| Line 34: | Line 34: | ||
K<sub>1</sub>(t) = K<sub>1</sub><sup>0</sup> + a t | K<sub>1</sub>(t) = K<sub>1</sub><sup>0</sup> + a t | ||
| − | k<sub>2</sub>(t) = | + | k<sub>2</sub>(t) = k<sub>2</sub><sup>0</sup> + b t |
| − | a and b are the derivatives (slopes) of the rate constant with respect to time. | + | K<sub>1</sub><sup>0</sup> and k<sub>2</sub><sup>0</sup> are the initial (0 superscript) values of the rate constants |
| + | and a and b are the derivatives (slopes) of the rate constant with respect to time. | ||
| − | To implement the time-varying rate constants, | + | To implement the time-varying rate constants, create a MATLAB function in a .m file. |
By making the function general, the same function can be used for K<sub>1</sub> and k<sub>2</sub>. | By making the function general, the same function can be used for K<sub>1</sub> and k<sub>2</sub>. | ||
| Line 81: | Line 82: | ||
| − | This function is pretty straightforward. The emphasis of our description here is on the mathematical | + | This function is pretty straightforward. The emphasis of our description here is on the mathematical details. |
The first output argument varargout{1} holds the value of the rate constant specified at the current time t. | The first output argument varargout{1} holds the value of the rate constant specified at the current time t. | ||
This value is first calculated and stored in the variable v. | This value is first calculated and stored in the variable v. | ||
| Line 302: | Line 303: | ||
| − | + | ==== Fitting the standard (time-invariant rate constants) model to data with changing physiology ==== | |
| − | + | Lets examine the consequences of fitting the standard (time-invariant rate constants) model to data wherein the | |
| − | the physiology (rate constants) are changing | + | the physiology (rate constants) are changing. Use the fancy model to create "data" and fit the standard model to that "data". |
<pre> | <pre> | ||
| Line 340: | Line 341: | ||
[[Image:ExampleFigureFDGTimeVaryingK1k2Fit.png]] | [[Image:ExampleFigureFDGTimeVaryingK1k2Fit.png]] | ||
| + | |||
| + | Examine estimated values of the rate constants | ||
| + | |||
| + | Parm. True (Init->Final) Est Est vs. Init Units | ||
| + | K<sub>1</sub> 0.150 -> 0.041 0.147 -2.3% 1/min | ||
| + | k<sub>2</sub> 0.325 -> 0.089 0.316 -2.8% 1/min | ||
| + | k<sub>3</sub> 0.050 0.048 -4.2% 1/min | ||
| + | k<sub>4</sub> 0.007 0.007 5.6% 1/min | ||
| + | k<sub>i</sub> 0.020 -> 0.020 0.019 -3.5% 1/min | ||
| + | |||
| + | It turns out that the estimated values are in close agreement with the values of the parameters at time zero (about the time of injection). | ||
| − | '''Note''' This code for this example can be found in | + | ==== Get the full example ==== |
| + | '''Note''' This code for this example can be found in '''fdgTimeVarying.m''' in the COMKAT examples folder. That version has a few extra bells and whistles that allow us, for example. to use the FDG model with or without k<sub>4</sub>. | ||
Revision as of 01:40, 28 March 2008
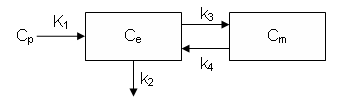
FDG Model with Time-varying Rate Constants
Overview
This example demonstrates how to implement the two-tissue compartment model with extended such that K1 and k2 vary in time.
This models the case where there are physiologic changes during the course of the PET scanning. This might happen if tumors are being treated during scanning.
The standard FDG model was described by Phelps and Huang .
It can also be described by the differential equations:
dCe/dt = K1 Cp - k2 Ce - k3 Ce + k4 Cm
dCm/dt = k3 Ce - k4 Cm
Ce is the tissue concentration of FDG and Cm as the tissue concentration of metabolized FDG (FDG-6-phosphate)
Ce and Cm are interpreted as molar concentrations (Salinas, Muzic and Saidel 2007).
In the standard model. the rate constants K1, k2, k3 and k4 are assumed to be independent of time.
Here we allow K1 and k2 to be linear functions of time:
K1(t) = K10 + a t
k2(t) = k20 + b t
K10 and k20 are the initial (0 superscript) values of the rate constants and a and b are the derivatives (slopes) of the rate constant with respect to time.
To implement the time-varying rate constants, create a MATLAB function in a .m file.
By making the function general, the same function can be used for K1 and k2.
function varargout = kinLinearTime(t, c, ncomp, nsens, pName, pValue, pSensIdx, cm, xtra)
% rate constant varies linearly with time: k = k0 + m*t where m = dk/dt
K0Name = pName{1};
dkdtName = pName{2};
K0Value = pValue{1};
dkdtValue = pValue{2};
K0SensIndex = pSensIdx{1};
dkdtSensIndex = pSensIdx{2};
if (nargout > 0), % return effective rate constant
v = K0Value + dkdtValue * t;
if (v < 0), % don't allow negative values for rate constant
varargout{1} = 0;
else
varargout{1} = v;
end
if (nargout > 1), % return dk/dc
dkdc = zeros([1 ncomp]);
varargout{2} = dkdc;
if (nargout > 2), % return dk/dp
dkdp = zeros([1 nsens]);
if (v >= 0),
dkdp(K0SensIndex) = 1;
dkdp(dkdtSensIndex) = t;
end
varargout{3} = dkdp; % dkdp
if (nargout > 3),
ddkdpdc = zeros([ncomp nsens]);
varargout{4} = ddkdpdc; % ddkdpdc
end
end
end
end
return
This function is pretty straightforward. The emphasis of our description here is on the mathematical details.
The first output argument varargout{1} holds the value of the rate constant specified at the current time t.
This value is first calculated and stored in the variable v.
v = K0Value + dkdtValue * t
k0 is the rate constant at time zero (t=0) and dkdtValue is the increase in the rate constant per unit time (time-derivative or slope). k0Value and dkdtValue are the MATLAB variables that hold the values of these parameters. The value of v is checked to see if it is negative and, if it is, the value zero is used instead since negative values for rate constants are non-physiologic.
The line
varargout{2} = dkdc;
returns the derivative of the rate constant with respect to all the compartment concentrations (a vector). In this case, the rate constant is not dependent on the concentrations so the derivatives are all zeros.
The lines
dkdp(K0SensIndex) = 1; dkdp(dkdtSensIndex) = t;
calculate the derivatives of the rate constant with respect to the model parameters k0 (the initial value of the rate constant) and dkdt (the increase in k per unit time). Since a model can have other parameters besides these, the function stores these derivatives in the appropriate element of the derivative vector. Derivatives of this rate constant with respect to all other parameters are zeros.
The line
varargout{4} = ddkdpdc; % ddkdpdc
returns the values of the mixed derivatives (derivative of rate constant with respect to concentrations and with respect to time), which, in this case are all zeros.
The function is stored in kinLinearTime.m in the comkat examples folder.
This function is called to evaluate both K1 and k2.
Implementing the Compartment Model
Create a new model
First define some MATLAB variables for clarity and to facilitate exploring what happens if values are changed
K10 = 0.15; % K1 = K10 + dK1dt * t dK1dt = -K10 * 0.5 / 60; % 50% decrease per 60 minutes k20 = 0.325; % k2 = k20 + dk2dt * t dk2dt = -k20 * 0.5 / 60; % 50% decrease per 60 minutes k3 = 0.05; k4 = 0.007;
Next, create a compartment model object and define the parameters within the model object
% create empty compartmentModel object cm = compartmentModel; % define the parameters cm = addParameter(cm, 'K10', K10); % 1/min cm = addParameter(cm, 'k20', k20); % 1/min cm = addParameter(cm, 'k3', k3); % 1/min cm = addParameter(cm, 'k4', k4); % 1/min cm = addParameter(cm, 'dK1dt', dK1dt); % 1/min/min cm = addParameter(cm, 'dk2dt', dk2dt); % 1/min/min cm = addParameter(cm, 'sa', 1); % specific activity of injection cm = addParameter(cm, 'dk', log(2)/109.8); % F-18 radioactive decay cm = addParameter(cm, 'PV', 1); % (none)
Now, define the model compartments. The first two are Ce and Cm as described above and Junk is a "sink" that collects the FDG that is cleared by the venous circulation.
cm = addCompartment(cm, 'Ce'); cm = addCompartment(cm, 'Cm'); cm = addCompartment(cm, 'Junk');
For the plasma concentration time-course of FDG or input function, we'll use the
Feng input
which is an analytic expression. Since piecewise polynomials (linear interpolation, cubic splines, etc...) are widely used in COMKAT and their implementation has been optimized,
here we construct a cubic spline representation of the input function by sampling the Feng input.
x0=[2 0.5 16.000 2.188 2.081 -7.5 -10 -0.01043]; % Feng parameters t = [0:.1:3 3.5 4 4.5 5:1:10 12 15:5:(expDuration+5)]; Cp = fengInput(x0, t); ppCp = spline(t, Cp); cm = addInput(cm, 'Cp', 'sa', 'dk', 'ppval', ppCp); % Cp has units of pmol/ml
The PET scanner measurement is assumed to represent the sum of FDG and FDG-6-Phosphate so the model output is calculated as the sum of the Ce and Cm compartments
Wlist = {...
'Ce', 'PV';
'Cm', 'PV'};
Xlist = {};
cm = addOutput(cm, 'PET', Wlist, Xlist);
Next define the scan frames as the start and stop time of each image in the dynamic sequence.
ttt=[ ones(12,1)*10/60; ... % 10 sec
ones(10,1)*0.5; ... % 0.5 min
ones(10,1)*2;... % 2 min
ones(10,1)*5;... % 5 min
ones(4,1)*10]; % 10 min
scant=[[0;cumsum(ttt(1:(length(ttt)-1)))] cumsum(ttt)];
cm = set(cm, 'ScanTime', scant);
Note the acquisition begins with 12 frames of 10 sec duration, then has 10 frames of 0.5 minute duration, etc... The cumsum() function calculates the cumulative summation. Thus, the first column of scant holds the scan start times and the second column holds the scan end times. These are expressed in minutes:
scant =
0 0.1667
0.1667 0.3333
0.3333 0.5000
0.5000 0.6667
0.6667 0.8333
0.8333 1.0000
1.0000 1.1667
1.1667 1.3333
1.3333 1.5000
1.5000 1.6667
1.6667 1.8333
1.8333 2.0000
...
Notice thus far the links (arrows) that connect the compartments have not been defined.
This has been delayed since we want to make two models: one will be the standard or reference model with time-invariant rate constants
and one with the time-varying K1 and k2. To make two models, we now make a copy of what we have so far
cmRef = cm;
For the reference model, define the links as time-invariant
% define reference model with time-invariant rate constants cmRef = addLink(cmRef, 'L', 'Cp', 'Ce', 'K10'); cmRef = addLink(cmRef, 'K', 'Ce', 'Junk', 'k20'); cmRef = addLink(cmRef, 'K', 'Ce', 'Cm', 'k3'); cmRef = addLink(cmRef, 'K', 'Cm', 'Ce', 'k4');
For the fancy model, define the links with the time-varying K1 and k2 rate constants
cm = addLink(cm, 'LSpecial', 'Cp', 'Ce', 'K1', 'kinLinearTime', {'K10', 'dK1dt'});
cm = addLink(cm, 'KSpecial', 'Ce', 'Junk', 'k2', 'kinLinearTime', {'k20', 'dk2dt'});
noting that these make use of the kinLinearTime.m function defined above.
Also, define the time-invariant links
cm = addLink(cm, 'K', 'Ce', 'Cm', 'k3'); cm = addLink(cm, 'K', 'Cm', 'Ce', 'k4');
OK, the models are ready for use. Begin by solving the model to obtain the time-courses of FDG activity that these models predict would be observed in PET images.
[PET, PETIndex] = solve(cm); [PETRef, PETRefIndex] = solve(cmRef);
Now plot the time-courses. Column 1 of PET (and PETRef) holds the frame start and end times. For convenience, compute the mid-frame time
tmid = (PET(:,1) + PET(:,2)) / 2;
And finally do the plotting
plot(tmid, PET(:,3), 'b', tmid, PETRef(:,3), 'b:');
xlabel('Time (Minutes)');
ylabel('Activity (uCi/ml)');
legend('Time-varying', 'Reference', 'Location', 'SouthEast');
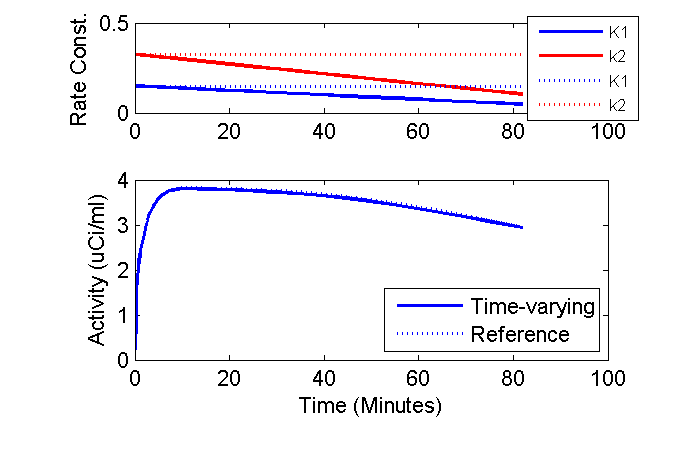
Well, we can get a bit fancy and plot the time-courses of the K1 and k2 rate constants above the model outputs and add other annotations.
clf
axK1k2 = axes('position', [0.2 0.75 0.7 0.2]);
phK = plot(axK1k2, tmid, K10 + dK1dt * tmid, 'b', tmid, k20 + dk2dt * tmid, 'r', ...
tmid, K10 + 0 * tmid, 'b:', tmid, k20 + 0 * tmid, 'r:');
set(phK, 'LineWidth', 1.5);
ax = axis; ax(3) = 0; ax(4) = 0.5; axis(ax);
ylabel('Rate Const. (1/min)');
lh = legend('K1', 'k2', 'K1', 'k2', 'Location', 'SouthEast');
set(lh, 'fontsize', 8);
axPET = axes('position', [0.2 0.2 0.7 0.4]);
phPET = plot(axPET, tmid, PET(:,3), 'b', tmid, PETRef(:,3), 'b:');
set(phPET, 'LineWidth', 1.5);
ax = axis; ax(3) = 0; axis(ax);
xlabel('Time (Minutes)');
ylabel('Activity (uCi/ml)');
legend('Time-varying', 'Reference', 'Location', 'SouthEast');
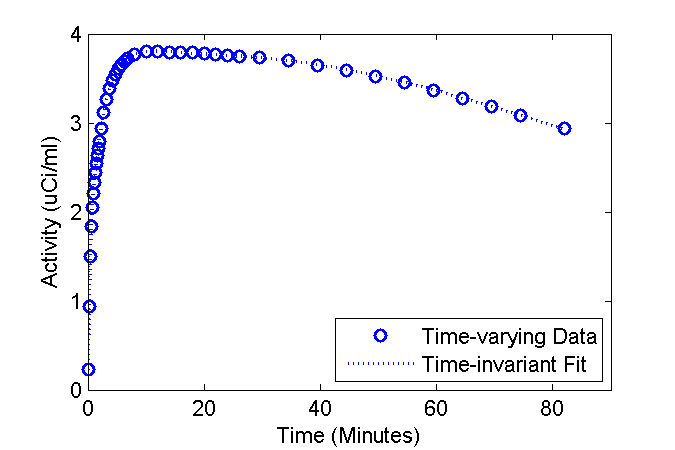
Fitting the standard (time-invariant rate constants) model to data with changing physiology
Lets examine the consequences of fitting the standard (time-invariant rate constants) model to data wherein the the physiology (rate constants) are changing. Use the fancy model to create "data" and fit the standard model to that "data".
data = PET(:,3); cmRef = set(cmRef, 'ExperimentalData', data);
Set the initial guess and lower and upper bounds on the rate constants
pinit = [0.07; 0.1; 0.04; 0.005]; % inital guess plb = [0.01; 0.001; 0.001; 0.0001]; % lower bound pub = [0.5; 0.5; 0.2; 0.01]; % upper bound cmRef = addSensitivity(cmRef, 'K10', 'k20', 'k3', 'k4');
Now do the fitting
[pfit, modelFit] = fit(cmRef, pinit, plb, pub);
Plot the fit over the "data"
figure
phFit = plot(tmid, data, 'bo', tmid, modelFit, 'b:');
set(phFit, 'LineWidth', 1.5);
ax = axis; ax(3) = 0; axis(ax);
xlabel('Time (Minutes)');
ylabel('Activity (uCi/ml)');
legend('Time-varying Data', 'Time-invariant Fit', 'Location', 'SouthEast');
Examine estimated values of the rate constants
Parm. True (Init->Final) Est Est vs. Init Units K1 0.150 -> 0.041 0.147 -2.3% 1/min k2 0.325 -> 0.089 0.316 -2.8% 1/min k3 0.050 0.048 -4.2% 1/min k4 0.007 0.007 5.6% 1/min ki 0.020 -> 0.020 0.019 -3.5% 1/min
It turns out that the estimated values are in close agreement with the values of the parameters at time zero (about the time of injection).
Get the full example
Note This code for this example can be found in fdgTimeVarying.m in the COMKAT examples folder. That version has a few extra bells and whistles that allow us, for example. to use the FDG model with or without k4.