Difference between revisions of "Support:Documents:Examples:Estimate Input Delay and Rate Constants"
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Estimating Input Delay and Rate Constants == | == Estimating Input Delay and Rate Constants == | ||
This example demonstrates an approach to simultaneously estimating input function delay along with parameters of the 1-tissue compartment (e.g. blood flow) model. | This example demonstrates an approach to simultaneously estimating input function delay along with parameters of the 1-tissue compartment (e.g. blood flow) model. | ||
| − | For the sake of generality, this could be interpreted as a | + | For the sake of generality, this could be interpreted as a dynamic contrast-enhanced (DCE) MRI or perfusion PET study. |
| Line 15: | Line 15: | ||
| − | where C<sub>T</sub> is the tissue concentration and C<sub>p</sub> is the plasma concentration | + | where C<sub>T</sub> is the tissue concentration and C<sub>p</sub> is the plasma concentration. |
C<sub>T</sub> and C<sub>p</sub> are interpreted as either molar concentrations ([http://www.ncbi.nlm.nih.gov/pubmed/17555251?ordinalpos=2&itool=EntrezSystem2.PEntrez.Pubmed.Pubmed_ResultsPanel.Pubmed_RVDocSum Salinas, Muzic and Saidel 2007]). | C<sub>T</sub> and C<sub>p</sub> are interpreted as either molar concentrations ([http://www.ncbi.nlm.nih.gov/pubmed/17555251?ordinalpos=2&itool=EntrezSystem2.PEntrez.Pubmed.Pubmed_ResultsPanel.Pubmed_RVDocSum Salinas, Muzic and Saidel 2007]). | ||
| Line 22: | Line 22: | ||
This example also demonstrates how to temporally align measured input function data to the tissue (image) data. Here the plasma concentration vs. time t is modeled as | This example also demonstrates how to temporally align measured input function data to the tissue (image) data. Here the plasma concentration vs. time t is modeled as | ||
| − | C<sub>p</sub>(t, tau) = M(t- | + | C<sub>p</sub>(t, tau) = M(t-tau) if t >= tau; 0 if t < tau . |
M(t) is the measured input data, tau is the delay parameter to estimate, and t is the time in minutes. | M(t) is the measured input data, tau is the delay parameter to estimate, and t is the time in minutes. | ||
| Line 28: | Line 28: | ||
Because the delay tau is estimated in this example, it will be handy to note that derivative of the input with respect to delay is | Because the delay tau is estimated in this example, it will be handy to note that derivative of the input with respect to delay is | ||
| − | + | dC<sub>p</sub>(t)/d tau = - dM/dt|<sub>t-tau</sub> | |
For this example, M is determined by using linear interpolation to interpolate between measured values. The interpolation is implemented using piecewise polynomial framework (and it could be easily modified to accommodate cubic spline interpolation). | For this example, M is determined by using linear interpolation to interpolate between measured values. The interpolation is implemented using piecewise polynomial framework (and it could be easily modified to accommodate cubic spline interpolation). | ||
| Line 73: | Line 73: | ||
The values of the parameters p = [K<sub>1</sub>; k<sub>2</sub>; tau] will be estimated. | The values of the parameters p = [K<sub>1</sub>; k<sub>2</sub>; tau] will be estimated. | ||
| − | '''Step 1''' Create a 1-tissue compartment model | + | '''Step 1''' To set the simulation in Matlab, create the above function and put in in a file called DelayExampleInput.m. |
| + | |||
| + | '''Step 2''' Create a 1-tissue compartment model | ||
<pre> | <pre> | ||
% create new, empty model | % create new, empty model | ||
| Line 132: | Line 134: | ||
midScanTime = (st(:,1) + st(:,2)) / 2; | midScanTime = (st(:,1) + st(:,2)) / 2; | ||
| − | % solve the model | + | % solve the model and generate the output |
[sol,solIndex] = solve(cm); | [sol,solIndex] = solve(cm); | ||
| + | plot(midScanTime,sol(:,3),'LineWidth',2); | ||
| + | xlabel('Minutes'); | ||
| + | ylabel('KBq/ml'); | ||
</pre> | </pre> | ||
| − | '''Step | + | [[Image:Pretest.jpeg]] |
| + | |||
| + | The above figure is the model output (C<sub>T</sub>). Here, we use it as perfect experimental data that would be fitted. | ||
| + | |||
| + | '''Step 3''' Use model output as measured C<sub>T</sub> (perfect "data") and fit it | ||
<pre> | <pre> | ||
% Set parameters: initial guess, lower and upper bounds for K1, k2 and tau | % Set parameters: initial guess, lower and upper bounds for K1, k2 and tau | ||
| − | pinit=[0. | + | pinit=[0.1;0.2;0.1]; |
lb =[0.01;0.01;0.01]; | lb =[0.01;0.01;0.01]; | ||
ub =[1;1;5]; | ub =[1;1;5]; | ||
| Line 153: | Line 162: | ||
</pre> | </pre> | ||
| − | '''Step | + | '''Step 4''' Examine model outputs using estimated parameter (pfit) and initial guess (pinit) |
<pre> | <pre> | ||
% Solve model using estimated parameters | % Solve model using estimated parameters | ||
| Line 162: | Line 171: | ||
est_sol=solve(cm1); | est_sol=solve(cm1); | ||
| − | plot(midScanTime,sol(:,3),'o',midScanTime,est_sol(:,3),'r-'); | + | % solve model using initial parameters |
| + | cm1=set(cm1,'ParameterValue','k1',pinit(1)); | ||
| + | cm1=set(cm1,'ParameterValue','k2',pinit(2)); | ||
| + | cm1=set(cm1,'ParameterValue','tau',pinit(3)); | ||
| + | est_sol_init=solve(cm1); | ||
| + | |||
| + | plot(midScanTime,sol(:,3),'o',midScanTime,est_sol(:,3),'r-',midScanTime,est_sol_init(:,3),'g-','LineWidth',2); | ||
xlabel('Minutes'); | xlabel('Minutes'); | ||
ylabel('KBq/ml'); | ylabel('KBq/ml'); | ||
| − | legend('Data', 'Fit'); | + | legend('Data', 'Fit','Initial Guess'); |
</pre> | </pre> | ||
| + | |||
| + | [[Image:test.jpeg]] | ||
Latest revision as of 04:46, 23 December 2008
Estimating Input Delay and Rate Constants
This example demonstrates an approach to simultaneously estimating input function delay along with parameters of the 1-tissue compartment (e.g. blood flow) model. For the sake of generality, this could be interpreted as a dynamic contrast-enhanced (DCE) MRI or perfusion PET study.
Tissue uptake
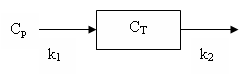
This model has one tissue compartment. Material in the blood is assumed to rapidly exchange with that in (extravascular) tissue. The tissue model has two rate constants: K1 and k2 and is depicted in the diagram:
It can also be described by the differential equation:
dCT/dt = K1 Cp - k2 CT
where CT is the tissue concentration and Cp is the plasma concentration.
CT and Cp are interpreted as either molar concentrations (Salinas, Muzic and Saidel 2007).
Input function
This example also demonstrates how to temporally align measured input function data to the tissue (image) data. Here the plasma concentration vs. time t is modeled as
Cp(t, tau) = M(t-tau) if t >= tau; 0 if t < tau .
M(t) is the measured input data, tau is the delay parameter to estimate, and t is the time in minutes.
Because the delay tau is estimated in this example, it will be handy to note that derivative of the input with respect to delay is
dCp(t)/d tau = - dM/dt|t-tau
For this example, M is determined by using linear interpolation to interpolate between measured values. The interpolation is implemented using piecewise polynomial framework (and it could be easily modified to accommodate cubic spline interpolation).
Let inputData be a two-column matrix with column 1 holding sample times and column 2 holding the sampled input concentrations.
The interpolation coefficients may be calculated using the lspline function
ppM = lspline(inputData(:,1), inputData(:,2));
To evaluate the derivative dCp/dt, which can be determined in terms of dM/dt by analytically differentiating the interpolating polynomial.
[breaks, coefs, l, k, d] = unmkpp(ppM); ppdMdtau = mkpp(breaks, repmat(k-1:-1:1,d*l,1) .* coefs(:,1:k-1), d);
The input function is then implemented as
function [Cp, dCpdtau] = DelayExampleInput(parm, t, X)
if (nargout > 0),
t = t(:); % ensure t is a column vector
tau = parm(1); % delay
ppC = X{1}; % piecewise-polynomial coefficients for Cp
Cp = zeros(size(t));
f = find(t > tau);
Cp(f) = ppval(ppC, t(f) - tau);
if (nargout > 1),
ppdCdt = X{2}; % piecewise-polynomial coefficients for derivative
dCpdtau = zeros(size(t));
dCpdtau(f) = -ppval(ppdCdt, t(f) - tau);
end
end
Example: Estimating Input Delay and Rate Constants
In this example, the model output are assumed to represent measurements of CT. (To keep the example simple, intravascular concentration of tracer is ignored.) The values of the parameters p = [K1; k2; tau] will be estimated.
Step 1 To set the simulation in Matlab, create the above function and put in in a file called DelayExampleInput.m.
Step 2 Create a 1-tissue compartment model
% create new, empty model
cm = compartmentModel;
% define default values for parameters
cm = addParameter(cm, 'k1', 0.3);
cm = addParameter(cm, 'k2', 0.5);
cm = addParameter(cm, 'tau', 0.25);
cm = addParameter(cm, 'sa', 1); % specific activity at t=0
cm = addParameter(cm, 'dk', 0.34); % decay constant
cm = addParameter(cm, 'tau', 0.25); % time delay
% add compartments
cm = addCompartment(cm, 'CT');
cm = addCompartment(cm, 'J');
% define the input(first column is time, second it concentration)
inputData = [
0 0
0.0500 0
0.1000 0
0.1500 14.5234
0.2000 52.1622
0.2500 76.6730
0.3000 91.6416
0.4000 103.0927
0.5000 100.9401
0.7000 83.5343
0.8000 74.3628
1.0000 59.7726
1.2500 48.7530
1.5000 43.0772
1.7500 40.1924
2.0000 38.6236
];
% determine spline coefficients for linear interpolation
ppM = lspline(inputData(:,1), inputData(:,2));
% analytically calculate derivative
[breaks, coefs, l, k, d] = unmkpp(ppM);
ppdMdtau = mkpp(breaks, repmat(k-1:-1:1,d*l,1) .* coefs(:,1:k-1), d);
X = {ppM, ppdMdtau};
cm = addInput(cm, 'Cp','sa','dk', 'DelayExampleInput', 'tau', X);
% connect compartments and inputs
cm = addLink(cm, 'L', 'Cp', 'CT', 'k1');
cm = addLink(cm, 'K', 'CT', 'J', 'k2');
% define the activity concentration in tissue pixel
cm = addOutput(cm, 'TissuePixel', {'CT','1'}, {'Cp','0'});
% specify scan frame times
st = [[0:5:85]' [5:5:90]']/60; % division by 60 converts sec to min
cm = set(cm, 'ScanTime', st);
midScanTime = (st(:,1) + st(:,2)) / 2;
% solve the model and generate the output
[sol,solIndex] = solve(cm);
plot(midScanTime,sol(:,3),'LineWidth',2);
xlabel('Minutes');
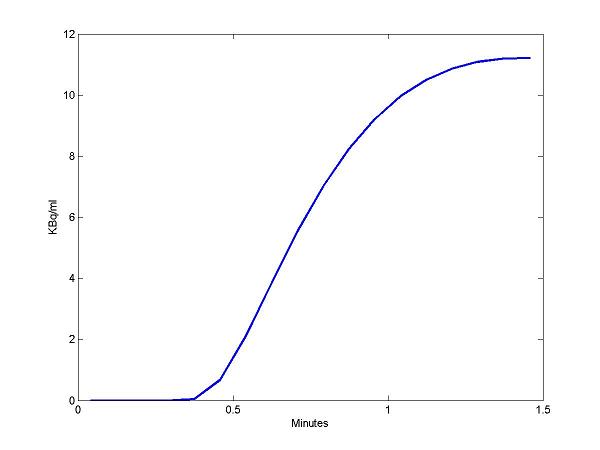
ylabel('KBq/ml');
The above figure is the model output (CT). Here, we use it as perfect experimental data that would be fitted.
Step 3 Use model output as measured CT (perfect "data") and fit it
% Set parameters: initial guess, lower and upper bounds for K1, k2 and tau pinit=[0.1;0.2;0.1]; lb =[0.01;0.01;0.01]; ub =[1;1;5]; % specify parameters to be adjusted in fitting cm=addSensitivity(cm,'k1','k2','tau'); % Experimental Data to be fit cm=set(cm,'ExperimentalData',sol(:,3)); % Perform curve fitting [pfit,qfitnull,modelfit,pp1,output]=fitGen(cm,pinit,lb,ub,'OLS');
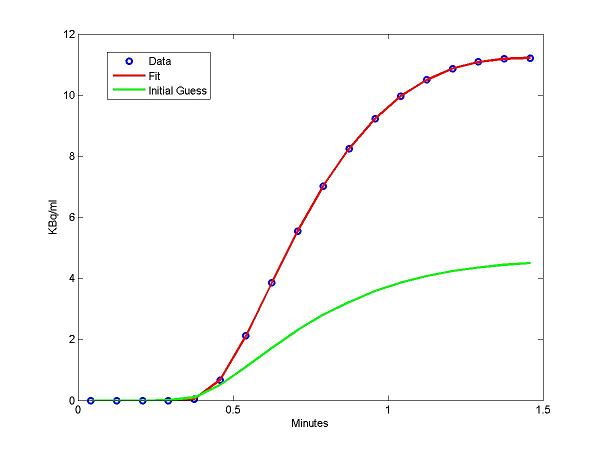
Step 4 Examine model outputs using estimated parameter (pfit) and initial guess (pinit)
% Solve model using estimated parameters
cm1=cm;
cm1=set(cm1,'ParameterValue','k1',pfit(1));
cm1=set(cm1,'ParameterValue','k2',pfit(2));
cm1=set(cm1,'ParameterValue','tau',pfit(3));
est_sol=solve(cm1);
% solve model using initial parameters
cm1=set(cm1,'ParameterValue','k1',pinit(1));
cm1=set(cm1,'ParameterValue','k2',pinit(2));
cm1=set(cm1,'ParameterValue','tau',pinit(3));
est_sol_init=solve(cm1);
plot(midScanTime,sol(:,3),'o',midScanTime,est_sol(:,3),'r-',midScanTime,est_sol_init(:,3),'g-','LineWidth',2);
xlabel('Minutes');
ylabel('KBq/ml');
legend('Data', 'Fit','Initial Guess');