Difference between revisions of "Support:Documents:Examples:Estimate Input Parameters, Rate Constants Known"
(New page: Here we assume that the input function has the form Cp = (p1t - p2 - p3) exp(-p4t) + p2 exp(-p5t) + p3 exp(-p6t) where Cp is the plasma concentration of 18FDG, pi are the input function...) |
|||
| (One intermediate revision by one other user not shown) | |||
| Line 56: | Line 56: | ||
% define compartments | % define compartments | ||
| − | cm = addCompartment(cm, 'Ce', | + | cm = addCompartment(cm, 'Ce',); |
| − | cm = addCompartment(cm, 'Cm | + | cm = addCompartment(cm, 'Cm'); |
| − | cm = addCompartment(cm, 'Junk | + | cm = addCompartment(cm, 'Junk'); |
% define plasma input function | % define plasma input function | ||
Latest revision as of 22:47, 18 December 2008
Here we assume that the input function has the form
Cp = (p1t - p2 - p3) exp(-p4t) + p2 exp(-p5t) + p3 exp(-p6t)
where Cp is the plasma concentration of 18FDG, pi are the input function parameters to be estimated, and t is time. (This form comes from Feng, Huang, Wang. "Models for Computer simulation Studies of Input Functions for Tracer Kinetic Modeling with Positron Emission Tomography", International Journal of Biomedical Computing, 32(2):95-110, March 1993.)
Step 1 To set this up in MATLAB for simulation, create the following function and put it in a file called refCp.m:
function [fval, jac] = refCp(p, t)
if (nargout > 0),
t = t(:); % make it a column vector
fval = (p(1)*t - p(2) - p(3)) .* exp(-p(4)*t) + p(2) * exp(-p(5)*t) + p(3) * exp(-p(6)*t);
if (nargout > 1),
jac = [t .* exp(-p(4)*t) ...
-exp(-p(4)*t) + exp(-p(5)*t) ...
-exp(-p(4)*t) + exp(-p(6)*t) ...
-t .* (p(1)*t - p(2) - p(3)) .* exp(-p(4)*t) ...
-t * p(2) .* exp(-p(5)*t) ...
-t * p(3) .* exp(-p(6)*t)];
end
end
return
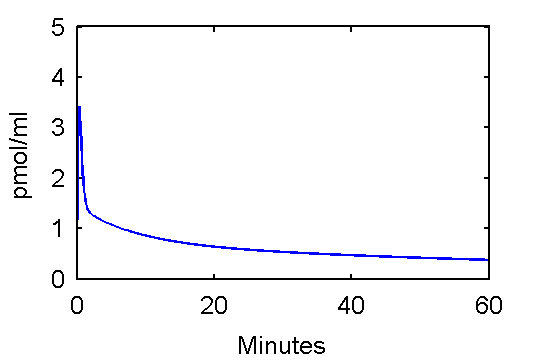
This function can be used to plot an example input curve using these commands
t=0:.1:60;
pin = [28 0.75 0.70 4.134 0.1191 0.01043];
plot(t,refCp(pin,t))
set(gca,'FontSize',6);
axis([0 60 0 5]);
xlabel('Minutes');
ylabel('pmol/ml');
Note that he above function, refCp.m not only calculates values Cp, it also optionally calculates values for the derivative of Cp with respect to parameter vector p. These will be needed later since to fit the input function, it is important to quantify how changes in values of p will effects Cp values which, in turn, effect model-predicted tissue concentration reflected in voxels or regions of interest.
Step 2 Create an FDG model
cm = compartmentModel;
% k1 k2 k3 k4
ktrue=[0.1020 0.1300 0.0620 0.0068];
% define the parameters
cm = addParameter(cm, 'k1', ktrue(1)); % 1/min
cm = addParameter(cm, 'k2', ktrue(2)); % 1/min
cm = addParameter(cm, 'k3', ktrue(3)); % ml/(pmol*min)
cm = addParameter(cm, 'k4', ktrue(4)); % 1/min
cm = addParameter(cm, 'sa', 75); % specific activity of injection, kBq/pmol
cm = addParameter(cm, 'dk', log(2)/109.8); % radioactive decay
cm = addParameter(cm, 'PV', 1); % (none)
% define input function parameter vector
cm = addParameter(cm, 'pin', [28; 0.75; 0.70; 4.134; 0.1191; 0.01043]);
% define compartments
cm = addCompartment(cm, 'Ce',);
cm = addCompartment(cm, 'Cm');
cm = addCompartment(cm, 'Junk');
% define plasma input function
% specifying function as refCp with parameters pin
cm = addInput(cm, 'Cp', 'sa', 'dk', 'refCp', 'pin'); % plamsa pmol/ml
% connect inputs and compartments
cm = addLink(cm, 'L', 'Cp', 'Ce', 'k1');
cm = addLink(cm, 'K', 'Ce', 'Junk', 'k2');
cm = addLink(cm, 'K', 'Ce', 'Cm', 'k3');
cm = addLink(cm, 'K', 'Cm', 'Ce', 'k4');
% specify scan begin and end times
ttt=[ ones(6,1)*5/60; ... % 6 frames x 5 sec
ones(2,1)*15/60; ... % 2 frames x 15 sec
ones(6,1)*0.5;... % 6 frames x 0.5 min
ones(3,1)*2;... % 3 frames x 2 min
ones(2,1)*5;... % 2 frames x 5 min
ones(10,1)*10]; % 10 frames x 10 min
scant = [[0;cumsum(ttt(1:(length(ttt)-1)))] cumsum(ttt)];
cm = set(cm, 'ScanTime', scant);
% define an output which is sum of Ce and Cm adjusted to account
% for partial volume (PV). Ignore vascular activity.
Wlist = {...
'Ce', 'PV';
'Cm', 'PV'};
Xlist = {};
cm = addOutput(cm, 'PET', Wlist, Xlist);
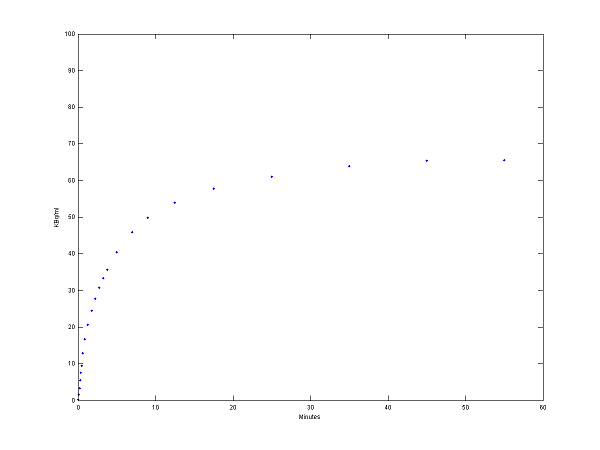
% solve model and generate example output
[PET, PETindex]=solve(cm);
plot(0.5*(PET(:,1)+PET(:,2)),PET(:,3), '.');
set(gca,'FontSize',6);
axis([0 60 0 100])
xlabel('Minutes');
ylabel('KBq/ml');
Step 3 Use model output as perfect "data"
data = PET(:,3);
Step 4 Fit the "data"
% tell model abbout data to be fit cm = set(cm, 'ExperimentalData', data); % specify parameters to be adjusted in fitting cm = addSensitivity(cm, 'pin'); % set parameter values initial guess, lower and upper bounds pinit = [ 10; 0.4; 0.4; 3; 0.05; 0.01]; plb = [ 10; 0.1; 0.1; 1; 0.05; 0.001]; pub = [100; 2. ; 2. ; 10; 1. ; 0.05]; % actually do the fitting pfit = fit(cm, pinit, plb, pub);
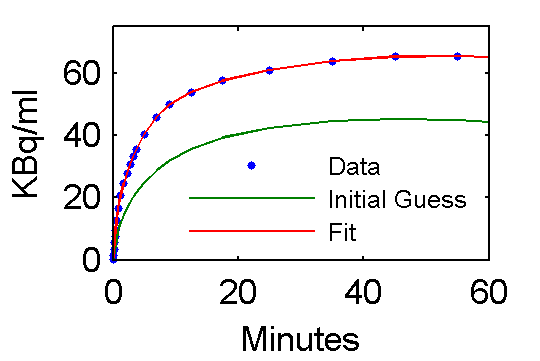
Values of parameter pfit estimates are [28.0167; 0.7652; 0.7059; 4.1586; 0.1257; 0.0105] and are reasonably close to the true values (pxEval(cm, 'pin')) [28; 0.75; 0.70; 4.134; 0.1191; 0.01043]
Step 5 Examine model outputs for "data", initial guess, and fit
PETfit = solve(set(cm, 'ParameterValue', 'pin', pfit));
PETinit = solve(set(cm, 'ParameterValue', 'pin', pinit));
t = 0.5*(PET(:,1)+PET(:,2));
plot(t,data,'.', t, PETinit(:,3), t, PETfit(:,3));
set(gca,'FontSize',8);
axis([0 60 0 75])
xlabel('Minutes');
ylabel('KBq/ml');
ah=legend('Data', 'Initial Guess', 'Fit','Location','SouthEast');
set(ah,'FontSize',6,'Box','off');