Difference between revisions of "Support:Documents:Examples:FDG with Time-varying Rate Constants"
(New page: == FDG Model with Time-varying Rate Constants == This example demonstrates how to implement the two-tissue compartment model with extended such that K1 and k2 vary in time. This models th...) |
|||
| Line 5: | Line 5: | ||
==== Tissue uptake ==== | ==== Tissue uptake ==== | ||
| − | This model was described by Huang | + | This model was described by Phelps and Huang. |
| + | |||
| + | '''MAKE FIGURE''' | ||
| − | |||
[[Image:ExampleFigureFDGModel.png]] | [[Image:ExampleFigureFDGModel.png]] | ||
| + | |||
It can also be described by the differential equations: | It can also be described by the differential equations: | ||
| Line 32: | Line 34: | ||
| − | To implement the time-varying rate constants, it is | + | To implement the time-varying rate constants, we create a MATLAB function in a .m file. |
| + | By making the function general, the same function can be used for K<sub>1</sub> and k<sub>2</sub>. | ||
| + | |||
| + | <pre> | ||
| + | function varargout = kinLinearTime(t, c, ncomp, nsens, pName, pValue, pSensIdx, cm, xtra) | ||
| + | % rate constant varies linearly with time: k = k0 + m*t where m = dk/dt | ||
| + | |||
| + | K0Name = pName{1}; | ||
| + | dkdtName = pName{2}; | ||
| + | K0Value = pValue{1}; | ||
| + | dkdtValue = pValue{2}; | ||
| + | K0SensIndex = pSensIdx{1}; | ||
| + | dkdtSensIndex = pSensIdx{2}; | ||
| + | |||
| + | |||
| + | if (nargout > 0), % return effective rate constant | ||
| + | v = K0Value + dkdtValue * t; | ||
| + | if (v < 0), % don't allow negative values for rate constant | ||
| + | varargout{1} = 0; | ||
| + | else | ||
| + | varargout{1} = v; | ||
| + | end | ||
| + | if (nargout > 1), % return dk/dc | ||
| + | dkdc = zeros([1 ncomp]); | ||
| + | varargout{2} = dkdc; | ||
| + | if (nargout > 2), % return dk/dp | ||
| + | dkdp = zeros([1 nsens]); | ||
| + | if (v >= 0), | ||
| + | dkdp(K0SensIndex) = 1; | ||
| + | dkdp(dkdtSensIndex) = t; | ||
| + | end | ||
| + | varargout{3} = dkdp; % dkdp | ||
| + | if (nargout > 3), | ||
| + | ddkdpdc = zeros([ncomp nsens]); | ||
| + | varargout{4} = ddkdpdc; % ddkdpdc | ||
| + | end | ||
| + | end | ||
| + | end | ||
| + | end | ||
| + | return | ||
| + | </pre> | ||
| + | |||
| + | |||
| + | This function is pretty straightforward. First we describe the mathematical aspects of it. | ||
| + | |||
| + | The first output argument varargout{1} holds the value of the rate constant specified at the current time t. | ||
| + | This value is first calculated and stored in the variable v. | ||
| + | <pre> | ||
| + | v = K0Value + dkdtValue * t | ||
| + | </pre> | ||
| + | |||
| + | k0 is the rate constant at time zero (t=0) and dkdtValue is the increase in the rate constant per uint time. | ||
| + | k0Value and dkdtValue are the MATLAB variables that hold the values of these parameters. | ||
| + | The value of v is checked to see if it is negative and, if it is, the value zero is used instead since negative values for rate constants are non-physiologic. | ||
| + | |||
| + | The line | ||
| + | <pre> | ||
| + | varargout{2} = dkdc; | ||
| + | </pre> | ||
| + | |||
| + | returns the derivative of the rate constant with respect to all the compartment concentrations (a vector). | ||
| + | In this case, the rate constant is not dependent on the concentrations so the derivatives are all zeros. | ||
| + | |||
| + | |||
| + | The line | ||
| + | <pre> | ||
| + | dkdp(K0SensIndex) = 1; | ||
| + | dkdp(dkdtSensIndex) = t; | ||
| + | </pre> | ||
| + | |||
| + | calculates the derivatives of the rate constant with respect to the model parameters k0 (the initial value of the rate constant) and dkdt (the increase in k per unit time). | ||
| + | Since a model can have other parameters besides these, the function stores these derivatives in the appropriate element of the derivative vector. Derivatives of this rate constant with respect to all other parameters are zeros. | ||
| + | |||
| + | |||
| + | The line | ||
| + | <pre> | ||
| + | varargout{4} = ddkdpdc; % ddkdpdc | ||
| + | </pre> | ||
| + | |||
| + | returns the values of the mixed derivatives (derivative of rate constant with respect to concentrations and with respect to time), which, in this case are all zeros. | ||
| + | |||
| + | The function is stored in kinLinearTime.m in the comkat examples folder. | ||
| + | |||
Revision as of 21:40, 27 March 2008
FDG Model with Time-varying Rate Constants
This example demonstrates how to implement the two-tissue compartment model with extended such that K1 and k2 vary in time.
This models the case where there are physiologic changes during the course of the PET scanning. This might happen if tumors are being treated during scanning.
Tissue uptake
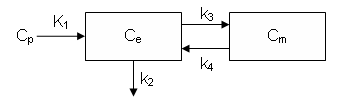
This model was described by Phelps and Huang.
MAKE FIGURE
It can also be described by the differential equations:
dCe/dt = K1 Cp - k2 Ce - k3 Ce + k4 Cm
dCm/dt = k3 Ce - k4 Cm
Ce is the tissue concentration of FDG and Cm as the tissue concentration of metabolized FDG (FDG-6-phosphate)
Ce and Cm are interpreted as molar concentrations (Salinas, Muzic and Saidel 2007).
In the standard model. the rate constants K1, k2, k3 and k4 are assumed to be independent of time.
Here we allow K1 and k2 to be a linear function of time:
K1(t) = K10 + a t
k2(t) = K20 + b t
To implement the time-varying rate constants, we create a MATLAB function in a .m file.
By making the function general, the same function can be used for K1 and k2.
function varargout = kinLinearTime(t, c, ncomp, nsens, pName, pValue, pSensIdx, cm, xtra)
% rate constant varies linearly with time: k = k0 + m*t where m = dk/dt
K0Name = pName{1};
dkdtName = pName{2};
K0Value = pValue{1};
dkdtValue = pValue{2};
K0SensIndex = pSensIdx{1};
dkdtSensIndex = pSensIdx{2};
if (nargout > 0), % return effective rate constant
v = K0Value + dkdtValue * t;
if (v < 0), % don't allow negative values for rate constant
varargout{1} = 0;
else
varargout{1} = v;
end
if (nargout > 1), % return dk/dc
dkdc = zeros([1 ncomp]);
varargout{2} = dkdc;
if (nargout > 2), % return dk/dp
dkdp = zeros([1 nsens]);
if (v >= 0),
dkdp(K0SensIndex) = 1;
dkdp(dkdtSensIndex) = t;
end
varargout{3} = dkdp; % dkdp
if (nargout > 3),
ddkdpdc = zeros([ncomp nsens]);
varargout{4} = ddkdpdc; % ddkdpdc
end
end
end
end
return
This function is pretty straightforward. First we describe the mathematical aspects of it.
The first output argument varargout{1} holds the value of the rate constant specified at the current time t. This value is first calculated and stored in the variable v.
v = K0Value + dkdtValue * t
k0 is the rate constant at time zero (t=0) and dkdtValue is the increase in the rate constant per uint time. k0Value and dkdtValue are the MATLAB variables that hold the values of these parameters. The value of v is checked to see if it is negative and, if it is, the value zero is used instead since negative values for rate constants are non-physiologic.
The line
varargout{2} = dkdc;
returns the derivative of the rate constant with respect to all the compartment concentrations (a vector). In this case, the rate constant is not dependent on the concentrations so the derivatives are all zeros.
The line
dkdp(K0SensIndex) = 1; dkdp(dkdtSensIndex) = t;
calculates the derivatives of the rate constant with respect to the model parameters k0 (the initial value of the rate constant) and dkdt (the increase in k per unit time). Since a model can have other parameters besides these, the function stores these derivatives in the appropriate element of the derivative vector. Derivatives of this rate constant with respect to all other parameters are zeros.
The line
varargout{4} = ddkdpdc; % ddkdpdc
returns the values of the mixed derivatives (derivative of rate constant with respect to concentrations and with respect to time), which, in this case are all zeros.
The function is stored in kinLinearTime.m in the comkat examples folder.
Implement the Compartment Model
Create a new model
First create an new model stored in variable bfcm (blood flow compartment model) and add compartments. The J compartment is not shown in the figure above but is needed to accept the flux from the k2 arrow.
% create new, empty model bfcm = compartmentModel; % add compartments bfcm = addCompartment(bfcm, 'CT'); bfcm = addCompartment(bfcm, 'J');
Specify the input
The specific activity (ratio of activity to molar concentration) is an exponentially decaying function S(t) = S0 exp(-0.341 t) where t is expressed in units of minutes and 0.341 = ln(2)/half-life of 15O and S0 is the specific activity at time t = 0.
% define the initial specific activity and decay constant sa0 = 1; % specific activity at t=0 dk = 0.341; % O-15 decay constant
Next specify the input functions Cp and Ca for the compartment model. fin is the name of the function that implements Feng input. pCp and pCa are parameter vectors that hold the values of p1, p2, ... p6 for Cp and Ca.
bfcm = addInput(bfcm, 'Cp', sa0, dk, 'fin', 'pCp'); bfcm = addParameter(bfcm, 'pCp', 2*[851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5]); bfcm = addInput(bfcm, 'Ca', sa0, dk, 'fin', 'pCa'); bfcm = addParameter(bfcm, 'pCa', [851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5]);
Define the connections (arrows) between the compartment and input. The link type 'L' indicates linear kinetics from an input to a compartment and type 'K' indicates linear kinetics from one compartment to another.
% connect compartments and inputs bfcm = addLink(bfcm, 'L', 'Cp', 'CT', 'K1'); bfcm = addLink(bfcm, 'K', 'CT', 'J', 'k2'); % define values for K1, k2 ... bfcm = addParameter(bfcm, 'K1', 'F'); bfcm = addParameter(bfcm, 'k2', 'K1/lambda'); bfcm = addParameter(bfcm, 'F', 0.5); bfcm = addParameter(bfcm, 'lambda', 1.0); bfcm = addParameter(bfcm, 'Fv', 0.05);
Define tissue and blood outputs
Define two model outputs. The output called TissuePixel predicts the activity in a tissue pixel and the output called ArterialPixel predicts the activity that would be observed in a pixel in the aorta. TissuePixel corresponds to CTS + FvCa whereas ArterialPixel is 100% Ca.
% define the activity concentration in tissue pixel
bfcm = addOutput(bfcm, 'TissuePixel', {'CT', '1'}, {'Ca', 'Fv'});
% define the activity concentration in arterial blood pixel
bfcm = addOutput(bfcm, 'ArterialPixel', {'CT', '0'}, {'Ca', '1'});
Note that COMKAT even accounts for the time-averaging of concentrations over the durations of the scan frames. For simplicity here a sequence of contiguous 10-second frames is used. (Frame start times 0, 10, 20, ... 590 sec and frame end times 10, 20, 30, ... 600 sec).
% specify scan frame times bfcm = set(bfcm, 'ScanTime', [[0:10:590]' [10:10:600]']/60); % division by 60 converts sec to min
Solve for the model output
Finally, tell COMKAT to solve the model to obtain simulation data that will be used in fitting.
[PET, PETIndex, Output, OutputIndex] = solve(bfcm);
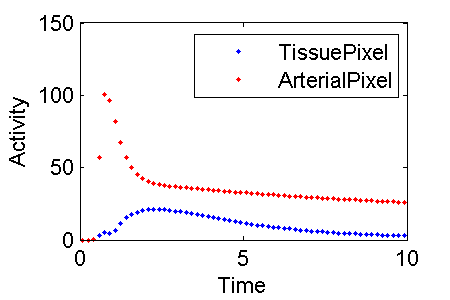
% plot activity in tissue PET(:,3) and blood PET(:,4)
midTime = (PET(:,1) + PET(:,2)) / 2;
plot(midTime, PET(:,3), 'b-', midTime, PET(:,4), 'r.')
legend(PETIndex{3}, PETIndex{4})
% make the figure for this wiki
set(1,'PaperPosition',[0.25 2.5 3 2])
print -dpng c:\temp\ExampleFigureBloodFlowInputModelDataToFit.png
Note, different rows of PET correspond to different frames. The columns of PET hold various quantities as indicated in PETIndex. That is, the contents of column i are described in PETIndex{i}.
Fit Data
Modify the COMKAT model a bit so that it can be used to fit data created above.
Specify the data to fit
Just use the result from above.
data = PET(:, [3 4]); bfcm = set(bfcm, 'ExperimentalData', data);
Specify parameters to estimate along with their initial guesses and range of feasible values.
% specify parameters to estimate bfcm = addSensitivity(bfcm, 'pCp', 'F'); % define initial guess and lower and upper bounds pCpInit = 0.9*2*[851.1 21.88 20.81 -4.134 -0.1191 -0.01043 .5]; FInit = 0.3; pinit = [pCpInit FInit]; lb = [2*[85 2 2 -8 -3 -0.1 .05] 0.1]; ub = [2*[2000 100 200 -1 -0.01 -0.001 2] 1.];
Note the values of the initial guesses for the input function parameters are 0.9 times the true values. (We're are not cheating by starting with the correct values.)
Do the actual fitting
Fit the data to estimate values of the parameters
[pEst, modelFit] = fit(bfcm, pInit, lb,ub);
COMKAT makes fitting easy!
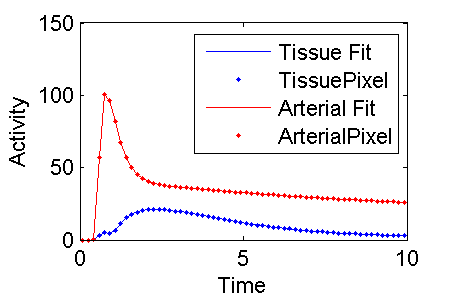
Plot the results and make the figure below for this wiki
plot(midTime, modelFit(:,1), 'b', midTime, PET(:,3), 'b.', midTime, modelFit(:,2), 'r', midTime, PET(:,4), 'r.')
legend('Tissue Fit', PETIndex{3}, 'Arterial Fit', PETIndex{4})
xlabel('Time')
ylabel('Activity')
print -dpng c:\temp\ExampleFigureBloodFlowInputModelFit.png
Ta Da
It looks like a pretty good fit.