Difference between revisions of "Support:Documents:Examples:Estimate Input Parameters Simultaneously with Flow"
(New page: == Create an example page == First, determine a page name for your example, such as "Instructions for Adding Your Own Example". The complete page name would be "Support:Documents:Examples:...) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
== Estimating Input Function Parameters Simultaneously with Flow == | == Estimating Input Function Parameters Simultaneously with Flow == | ||
This example demonstrates an approach to simultaneously estimating input functions parameters along with blood flow in the context of the PET blood flow model. | This example demonstrates an approach to simultaneously estimating input functions parameters along with blood flow in the context of the PET blood flow model. | ||
| + | |||
| + | ==== Tissue Uptake ==== | ||
The flow model has one tissue compartment and (radioactive) water in the blood is assumed to rapidly exchange with the water in the tissue. | The flow model has one tissue compartment and (radioactive) water in the blood is assumed to rapidly exchange with the water in the tissue. | ||
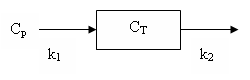
| − | The tissue model has two rate constants: K<sub>1</sub> and k<sub>2</sub> | + | The tissue model has two rate constants: K<sub>1</sub> and k<sub>2</sub> and can be depicted in a diagram: |
[[Image:ExampleFigureBloodFlowModel.png]] | [[Image:ExampleFigureBloodFlowModel.png]] | ||
| + | |||
| + | It can also be described by the differential equation: | ||
| + | |||
| + | dC<sub>T</sub>/dt = K<sub>1</sub> C<sub>p</sub> - k<sub>2</sub> C<sub>T</sub> | ||
| + | |||
| + | |||
| + | where C<sub>T</sub> is the tissue concentration and C<sub>p</sub> is the plasma concentration of radioactive water. | ||
| + | |||
Instead of estimating K<sub>1</sub> and k<sub>2</sub>, it sometimes is advantageous estimate a different set of parameters defined as | Instead of estimating K<sub>1</sub> and k<sub>2</sub>, it sometimes is advantageous estimate a different set of parameters defined as | ||
| Line 13: | Line 20: | ||
lambda = K<sub>1</sub>/k<sub>2</sub> and F = K<sub>1</sub>. | lambda = K<sub>1</sub>/k<sub>2</sub> and F = K<sub>1</sub>. | ||
| − | + | F is blood flow (perfusion) per unit volume of tissue (we're assuming 100% extraction) and lambda is the ratio of tissue to blood concentration at equilibrium. | |
| + | |||
| + | To use this parameterization in COMKAT, one needs to express the rate constants in terms of lambda and F: | ||
| + | K<sub>1</sub> = F, k<sub>2</sub> = K<sub>1</sub>/lambda | ||
| + | |||
| + | This example demonstrates how to estimate lambda and F. | ||
| + | |||
| + | |||
| + | ==== Input Function ==== | ||
| + | This example also demonstrates how to use a parameterized input function. Specifically, the plasma concentration vs. time is modeled as | ||
| + | |||
| + | C<sub>p</sub> = (p<sub>1</sub>t - p<sub>2</sub> - p<sub>3</sub>) exp(p<sub>4</sub> t) + p<sub>2</sub> exp(p<sub>5</sub> t) + p<sub>3</sub> exp(p<sub>6</sub>t) [aka Feng input] | ||
| − | + | This input function was proposed in Feng ''Int. J. Biomed. Comput.'' 32(2):95-110, 1993 and has been implemented in fin.m in the COMKAT examples folder. | |
| − | + | ==== Pixel Values ==== | |
| − | + | In a PET image, pixel values represent the radioactivity concentration. There are contributions from radioactivity in blood and tissue. The arterial blood concentration includes radioactive water in plasma and the blood cells and is designated C<sub>a</sub>. Here we assume C<sub>a</sub> can be described using the Feng input equation but with different values for p<sub>1</sub>, p<sub>2</sub>, ... p<sub>6</sub> than were used for C<sub>p</sub>. | |
| + | The tissue concentration is C<sub>T</sub> and is given above. The pixel activity concentration is calculated as the concentration in the tissue plus the pixel's fractional blood space F<sub>v</sub> times the arterial blood concentration: C<sub>T</sub> + F<sub>v</sub>C<sub>a</sub>. | ||
| + | == COMKAT Implementation == | ||
| + | T | ||
| − | |||
==== Text ==== | ==== Text ==== | ||
Revision as of 20:01, 7 March 2008
Estimating Input Function Parameters Simultaneously with Flow
This example demonstrates an approach to simultaneously estimating input functions parameters along with blood flow in the context of the PET blood flow model.
Tissue Uptake
The flow model has one tissue compartment and (radioactive) water in the blood is assumed to rapidly exchange with the water in the tissue. The tissue model has two rate constants: K1 and k2 and can be depicted in a diagram:
It can also be described by the differential equation:
dCT/dt = K1 Cp - k2 CT
where CT is the tissue concentration and Cp is the plasma concentration of radioactive water.
Instead of estimating K1 and k2, it sometimes is advantageous estimate a different set of parameters defined as
lambda = K1/k2 and F = K1.
F is blood flow (perfusion) per unit volume of tissue (we're assuming 100% extraction) and lambda is the ratio of tissue to blood concentration at equilibrium.
To use this parameterization in COMKAT, one needs to express the rate constants in terms of lambda and F: K1 = F, k2 = K1/lambda
This example demonstrates how to estimate lambda and F.
Input Function
This example also demonstrates how to use a parameterized input function. Specifically, the plasma concentration vs. time is modeled as
Cp = (p1t - p2 - p3) exp(p4 t) + p2 exp(p5 t) + p3 exp(p6t) [aka Feng input]
This input function was proposed in Feng Int. J. Biomed. Comput. 32(2):95-110, 1993 and has been implemented in fin.m in the COMKAT examples folder.
Pixel Values
In a PET image, pixel values represent the radioactivity concentration. There are contributions from radioactivity in blood and tissue. The arterial blood concentration includes radioactive water in plasma and the blood cells and is designated Ca. Here we assume Ca can be described using the Feng input equation but with different values for p1, p2, ... p6 than were used for Cp. The tissue concentration is CT and is given above. The pixel activity concentration is calculated as the concentration in the tissue plus the pixel's fractional blood space Fv times the arterial blood concentration: CT + FvCa.
COMKAT Implementation
T
Text
Write some introduction to your example.
Code
You can put code in a different format using <pre> tags like:
For text that you want to appear as part of a MATLAB function or program, encase it inside a "pre" block.
Line 2 of pre block
Line 3 (indented) of pre block.
Edit the current page to see how this is done.
Figures
Remember to include figures and plots in your example to make it look pretty and convey information. To insert a figure, create a figure file in png (preferred) or other graphic format.
figure
plot(1:10)
title('Example Figure')
ylabel('y-axis label')
xlabel('x-axis label')
set(1,'PaperPosition',[0.25 2.5 3 2])
print -dpng ExampleFigure.png
Next, upload the image file ("upload file" at the bottom of any wiki page) giving it a unique name.
Use double-square brackets to insert the figure into the page
Edit the example index page to include your example in the list
Add your new example to the list of examples on the example index page by adding a line like this to the index page:
[http://comkat.case.edu/comkat/comkat_wiki/index.php?title=Support:Documents:Examples:Instructions_for_Adding_Your_Own_Example The title of you example]
Within the brackets, the first part is the URL address to your example page. Then you type your example title following that address. On the index page it will look like:
That is it. It is so simple that even a caveman (or professor) can do it.